We Got A Problem #2: The current time is… 120 degrees

The hour, minute, and second hands of a continuously-moving clock all point the same direction at 12 noon.  But when are they equally spaced around the clock face?

In attacking this problem, Kathy from Pittsburgh pointed out that at 12:20:40, the hands almost form three 120-degree angles.  But they don’t, because the hour hand has moved a little passed 12 on its way to 1, and the minute hand has moved a little too.

So, when do the three clock hands form three 120-degree angles?

We’d love for readers to be able to explore this problem, so resist the urge to provide answers in the comments. Instead, we’d love helpful suggestions and ideas about different ways to approach the problem, successful or not. If you’d like to provide a full solution, do so with a pingback to your own blog!

We Got A Problem #1: 6/5/11

Today is June 5, 2011, or 06-05-11 in shorthand (05-06-11 in many countries).

Interestingly, 06 + 05 = 11.  How many more times in this century will it happen that the month number plus the day number equal the last two digits of the year number?

We’d love for readers to be able to explore this problem, so resist the urge to provide answers in the comments.  Instead, we’d love helpful suggestions and ideas about different ways to approach the problem, successful or not.  If you’d like to provide a full solution, do so with a pingback to your own blog!

Guess-Check-Generalize and the Scrubbing Calculator

Several other blogs have been talking about Bret Victor’s Kill Math website, including its Scrubbing Calculator.  I’d like to talk about how the Scrubbing Calculator is both very similar to and very different from an approach to solving word problems we call “Guess-Check-Generalize”.  Here’s a graphic from a sample problem solved Scrubbingly.

The challenge is to find the height of each bar, given the information about other heights.  When I first taught Algebra 1, my approach to this would be to get students to “translate” the problem into algebra, trying to get them to write an equation that would be true for the right height.  And the results were a mixed bag, for a lot of reasons that might be good for a different post.  I think there’s something inherently challenging about trying to write a fully symbolic statement immediately from a problem situation.

The concept of guess-check-generalize starts by changing the nature of the problem.  The question to start with changes:

from What is the correct bar height? …

to Is 100 the correct bar height?

Here, 100 could have been any number at all, it’s a total guess.  (Some teachers using this method ask students to write down their first guess before even presenting the problem, since students may be afraid to guess incorrectly.)

Now we see if the guess is right.  Up until now, I agree completely with the philosophy of the Scrubbing Calculator: make a guess at the bar height, then see if it’s right.  This is where things get interesting, because there’s more than one way to check the guess.  The most conventional way is to add up the heights on the right side, and a student might do this:

60 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 20 + 100 + 140 = nope

It doesn’t actually matter what that equals, as long as it doesn’t equal 768.  Guess-check-generalize is about determining a process you can use to check any guess; then, the process you’ve described becomes an equation to solve.  And the process can evolve from one guess to another, as students realize they’ve used the same number 8 times or that this thing is twice that thing.

So 100 was wrong; take a second guess.  It doesn’t have to be a better guess, because you’re not trying to nail the numeric answer, you’re trying to nail the process of checking a guess.  Let’s guess 36.  Checking this guess a student might notice they could combine some terms from before:

No more guessing.  The third guess is 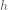, a variable.  (Students may need more guesses, especially at first; eventually some only need one or zero guesses.)  Take all the places the guess was found and replace them with the variable, noting that the correct guess yields 768:

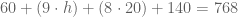
Solving that equation and bringing the answer back into context are still issues, but I always found the largest difficulty with the dreaded “word problem” is an inability to take the situation and make a mathematical statement about it.  When almost every real mathematical situation an adult encounters is a “word problem”, this is a major issue that needs to be addressed.

Here’s why I think guess-check-generalize is a good way of dealing with word problems.

• The method is general in nature.  The method presented here works equally well for linear and nonlinear situations, for problems with a variable on each side of the equation, for rates, coin values, painting houses, counting beans, whatever.  This is a general-purpose tool that is useful over many years, including some surprising topics like generating the equations of lines and circles.  (More on this some other time.)
• This is what people do with problems.  When a problem is new or overly complicated, picking a few cases and following them through leads to an understanding of what happens in general.  Traditional word problem methods expect students to have the generalization at the ready, and it just doesn’t work that way in reality.  The concept of generalizing from repeated example is a fundamental one that all students should learn, not just those heading into STEM careers.
• Students have a simple place to start from.  By asking students to guess at the answer, the difficulty level of word problems can be reduced by 2 or 3 grade levels immediately.  Students with language difficulty can learn what is happening by calculating with numbers, connecting the new language to the calculations they know, then advancing to symbols when appropriate.
• There are no black boxes.  Students construct equations and can understand where they come from.  Multiple equations with the same answer can be found from different techniques used on the same problem, leading to good discussions about the basic moves of algebra and how different equations and formulas are related.
• Connections between arithmetic and algebra are reinforced.  Bret Victor says this: “We are accustomed to assuming that variables must be symbols. But this isn’t true — a variable is simply a number that varies.”  I’d like this to change.  Too many students only see variables as symbols for manipulation, and not as numbers that vary.  Students make mistakes with variables they would never make with numbers.  When this happens, it is because they don’t see that the symbol represents a number.  Since arithmetic is at the heart of guess-check-generalize, students are asked to solidify their number skill and sense.  Students begin to guess “nice” numbers, like a multiple of 3 when they see that dividing by 3 will be part of the process.

It is on this last point that I disagree deeply with the philosophy of the Scrubbing Calculator; students don’t really do any of the calculating.  In the end, a student might see that the answer produced by Scrubbing works, but if there is more than one answer, there’s no way for a student to discern this.  If the problem changes slightly from its original form (say, to a 1024-high screen), the Scrubbing solution method is to start from scratch, which doesn’t help students generalize toward functions and formulas (in this case, a relationship between the screen height and the bar height).

What if the correct answer to the equation is 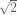or even ?  I don’t see how the Scrubbing Calculator could get these answers.  I agree that too many students don’t see the real meaning of a variable, but this is no reason to ditch symbolic algebra, this is a reason to make the connections between arithmetic and algebra as strong as possible, as often as possible.

The Scrubbing Calculator’s method is an opportunity for students to make deep connections between arithmetic and algebra, between real problems and symbolic algebra.  I’m disappointed that its intended purpose is to remove symbolic algebra altogether, because it could be pretty cool.  What do you think?

For homework, solve this problem using guess-check-generalize or come up with a better one.  No scrubbing, please!

Nancy takes a long car trip from Boston.  In one direction she drives at an average speed of 60 miles per hour, and in the other direction she drives at an average speed of 50 miles per hour.  She’s in the car a total of 38 hours for the round trip.  How far from Boston was her destination?  (Bonus: what city did she drive to?)