Articles from Art of Problem Solving!

I wrote these three articles on mathy things in pop culture:

The Math of Among Us: https://artofproblemsolving.com/resources/among-us

The Math of Winning Wordle: https://artofproblemsolving.com/blog/articles/the-math-of-winning-wordle

The Math of Big-Money Lotteries: https://artofproblemsolving.com/blog/articles/the-math-of-big-money-lotteries

Assessment Principles in Illustrative Mathematics 6-8 Math

A wide-ranging team worked together to develop the Illustrative Mathematics Grades 6-8 Math curriculum. As Assessment Lead, it was my responsibility to write and curate the Shared Understandings document about assessments we used throughout the writing process, and I thought you might be interested to read some of the key features.

This quote drives a lot of the ideas about assessment:

“You want students to get the question right for the right reasons and get the question wrong for the right reasons.” – Sendhil Revuluri

The statement above is particularly true for multiple-choice items, and is a shift from the ways I used to write as a high school teacher. If there were a likely “sign error” I would include that as a multiple-choice distractor, because surely some students will make that mistake. But this is the wrong reason to be wrong: the item is meant to test a particular standard. Distractors should have good reasons for being selected that are relevant to the standard(s) being addressed.

• In general, assessment items should be targeted and short.

This particularly is true for application problems, which frequently have sentences or paragraphs that are meaningless to the task at hand.

• Items must exist in isolation, never using the result of another item. These “double whammy” items penalize students who make an error or skip items. Each part of an extended response item must not depend on answering a previous part correctly. Each part should be answerable even if all previous parts have been skipped completely, to give students all possible opportunities to show proficiency. When you think a “double whammy” is unavoidable, think about what information would put the student in the position that a student correctly answering the first part would be. Typically, a “restart” of the item with a different name, object, equation, or example of the same context can avoid the “double whammy”.

Specifically, never ask students to use their work in part (a) to do part (b), because if they could not solve part (a), they have no ability to demonstrate the skill intended by part (b).

• Items must be method-agnostic whenever possible. Avoid “Use [method] to solve [problem]”, because this may force students to use a method or representation that runs against their preferences.

Just write “Solve [problem]”.

• Assessments as a whole should reflect a varied depth of knowledge including items that would be rated as DOK 1, 2, or 3 on this chart. In general, an assessment should have about 40% DOK 1, 40% DOK 2, and 20% DOK 3. The most typical error is not enough DOK 1.

It’s okay to include a few fastballs on a test!

• A student who has mastered the target skill should ideally be able to answer a multiple-choice item without looking at the options, then find the answer among the options. In some cases it is necessary to have the student discriminate among the options, but if this can be avoided, do so. For example, “Which of these points is in Quadrant II?” can be improved by asking “Which quadrant is (-3,4) in?”

And this is the biggest one for multiple-choice:

• Think carefully about the logic a student might use to respond to the item, and whether there are significant and relevant conceptual errors a student could make but still arrive at the correct response. Pick correct responses accordingly, or use distractors to catch these errors. For example, consider “Which of these fractions is largest? 1/3, 1/4, 2/7, 3/8”. It seems fine, but a student whose process is “a fraction with a larger numerator is larger” will select 3/8 and would be correct for the wrong reason. In this case 2/5 would be a better correct answer (replacing 2/7); if 3/8 is the intended correct response, use at least one distractor with a larger numerator.

There is a lot more to say, but hopefully this gives you some flavor for the depth of thought the Illustrative Mathematics team put into these materials. Go here for access to the materials. Thanks for reading!

Is 2501 prime?

While walking the dog I encountered the license plate “A 2501”, and because I’m a weirdo my immediate question was to wonder if 2501 is prime.

It’s not a multiple of 3… or 7… or 13.

So, let’s give you some spoiler space, to try the problem without any techmology. Is 2501 prime, or not?

 

 

 

This spoiler space is sponsored by the Illustrative Mathematics Grades 6-8 curriculum, coming very soon! It will be CC-BY, which means you can download and use it free for any purpose, forever.

 

 

 

Enough space yet?

 

 

So, having failed to find a simple multiple that divides 2501, I noticed it was one more than a multiple of 4, and a sum of squares:

This is a sign that it might be prime, because all primes that are one more than a multiple of 4 can be written as the sum of two squares (try 17 … 21 … 29). But it’s also a sign that it might not be prime, because all primes that are one more than a multiple of 4 can be written as the sum of two squares in exactly one way (try 25 … 65).

So the search changed from finding a factor to finding another sum of squares, and the search ended quickly after remembering 2401 was a perfect square:

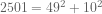
What’s interesting here is we know from this that 2501 is not prime, but we don’t know what its factors are! Having tested and not finding any prime factors less than 17, this is enough to know that 2501 is the product of exactly two prime factors.

But which ones? To do this, I tried to find a way to write 2501 as a difference of squares. And again, the search ended much more quickly than I expected:

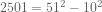
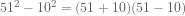
It made me wonder if there are other numbers with the same property, where the number is 1 more than a perfect square, and also has an equal gap to the next square up and next square down… guess what.

26 between 16 and 36

37 between 25 and 49

between  and 

Let me know if you find anything interesting here, or if you have any favorite numerical calculations like these.

All-New Mathematics of Game Shows (NCTM 2016)

Thanks to those who attended my talk at NCTM 2016 at 8am Saturday! Yow, that’s early. At the same time as many other great talks, it was an honor to have a good audience.

Here are the slides from my presentation. Hopefully they make sense to those who weren’t there, but if you have any questions, please let me know.

Slides from NCTM 2016 (PDF)

Ed Begle’s Laws of Mathematics Education

This post from Dan Meyer discussed Ed Begle’s two laws of mathematics education, which feel as relevant today as they did during his presentation in October 1970.

1. The validity of an idea about mathematics education and the plausibility of that idea are uncorrelated.
2. Mathematics education is much more complicated than you expected even though you expected it to be more complicated than you expected.

You can read all of Begle’s remarks beginning at page 27 of this document, which also includes many other presentations and papers from the same conference.

On speed and fluency

I really enjoyed this article by former NCTM president Cathy Seeley, “Faster Isn’t Smarter”. It’s been interesting over the years to get to talk to many mathematicians that did not feel like they were good at math as children, because of their relatively slow speed.

Fluency matters, but it’s not real surprising that students expect all math problems to be solvable within seconds if they are given thousands of problems that are solved within seconds, and rewarded for how quickly or how many they can do within a time limit. Seeley also discusses issues that emerge in a timed, high-stress environment:

“Some students respond well to competitive and timed situations, thriving on the pressure to bring out their best; others have quite a different reaction. This particular boy received a clear message that some students are good at math and some are not—and he knew which group he was in. He also was prevented from finishing the test, something that causes some students tremendous frustration.”

The article offers some simple suggestions for changing this dynamic in favor of fluency without focusing on speed. Thanks!

From Paul Goldenberg, on mathematics learning and languages

I had a conversation with Grace Chen and Christopher Danielson, among others, about how languages can affect students’ early learning of mathematics. For example, in Mandarin the phrasing for twelve is equivalent to “one ten two” in English.

Paul Goldenberg sent me this and I got his permission to publish it here. Thanks Paul!

—

I don’t know of any language that uses an essentially spelling pronunciation of the numerals (e.g., 23 as “two three”) although that is essentially what common (out-of-school) practice does with decimals. Only U.S. elementary schools insist that 3.1416 be pronounced “three and one-thousand sixteen ten thousandths.” (It is, or at least was in 2006, required of school teachers in Austin, Texas.)

But I did say that there were many variants on fully or nearly place-value pronunciations.  French ranks near 0 (with near regularity in low numbers not beginning until 16 and succumbing to IE’s general love of toes later on; 91 is four twenties eleven), Danish is slowly reforming from a 5 to a 6, English a 6 or 7.  But, for example, Kinyarwanda does 11 (etc.) as “ten and one” and has only minor anomalies in the naming of numbers (20, as in French, is not built the way larger multiples of 10 are built, though it is far more recognizably two-ish than the French is).

The use of numbers for counting, and for counting things, differs in some languages where agreement with noun gender (or other class) is required, but people are so used to accounting for the affixes that they’re almost invisible (inaudible?) anyway.

But the regularity in structure seems to be more important than regularity in application.  For example, Kinyarwanda’s regularity in structure (and, I suppose, the fact that tiny kids handle money in the hundreds and thousands) gets kids really good really early. Their first graders are better at counting by ones and tens (the latter even if we start at 4 or 7 and proceed to 14 or 17, etc.) than many kids here.  And that’s despite the fact that number-noun agreement requires some eight (I think I’m getting that right) different grammatical forms. (Bleh!)

What I do know firsthand is how differently children respond to print than to spoken (mental) calculations set in some (not necessarily “concrete”) context.  I don’t think it has anything to do with abstract vs. concrete, but rather about some existing semantics.  For example, adding 9 in the context of adding 10 is a no-brainer for kids, but it takes them much longer to look at 23 + 9, especially if it’s set up vertically, and think of doing anything other than what they were taught to do—recalling a specific fact and going through specific notational moves—and they can easily blow steps that have no semantic sense and only syntax (rules and order) to guide them.

From Al Cuoco, examples of the Standards for Mathematical Practice in algebra

Here’s a short piece by EDC’s Al Cuoco on the use of Common Core’s 8 Mathematical Practices as applied to algebra.

Download PDF

Million Dollar Mathematics of Game Shows from NCTM 2015

At NCTM 2015 I gave a talk on the mathematics of game shows, including Deal or No Deal and several games from The Price Is Right: 1/2 Off, Master Key, and Plinko.

We discussed some of the choices made in designing these games and others, and how the most interesting questions about shows are from the producers’ side, not the contestants’ side.

We also played games and I attempted to give away lots of money. Sadly, most of the games were lost.

Below is a PDF with the slides from the talk. I will repost the slides from the previous NCTM game show talks soon.

Thanks! I’ve been asked a few times — yes, I’m happy to present this or any other talk for a school or district, for students or teachers.

Mathematics of Game Shows 2015

From Al Cuoco, a commentary on formal algebra and bookkeeping

Some interesting thoughts by Al Cuoco about polynomial arithmetic and how Taylor series can be used to solve some interesting problems.

Formal Algebra (PDF)