We Got A Problem #13: Deal or No Deal

This short game is played with ten playing cards: an ace, two, three, …, nine, and a joker.  I shuffle the cards and lay them face down.

Your decision: grab as many cards as you want, still face down. When you’re ready, flip them all over at once and win: $1 multiplied by the sum of the card values.

Except the joker. If you flip over the joker, you win nothing. Good day.

So, how many cards should you take to maximize your expected return? What would change if all nine non-joker cards were aces? Eight aces and a ten?

[Testing Testing] SBAC Grade 11 Practice Test #4

Each “Testing Testing” post analyzes a released test item, focusing on both the mathematics and interface involved in the new breed of exams. Our goal is to help improve the quality of these exams, especially if they may be used to inform student graduation or teacher merit pay. The mathematical analysis here is from Al Cuoco, director of the Center for Mathematics Education at EDC, from the Trevi Fountain in Rome. I provide the interface analysis.

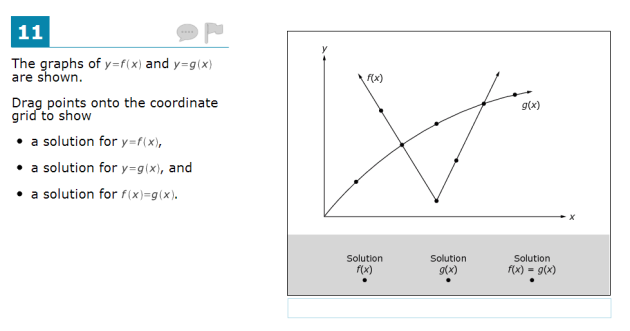
Here’s Problem 4 from the SBAC Grade 11 Math Practice Test.

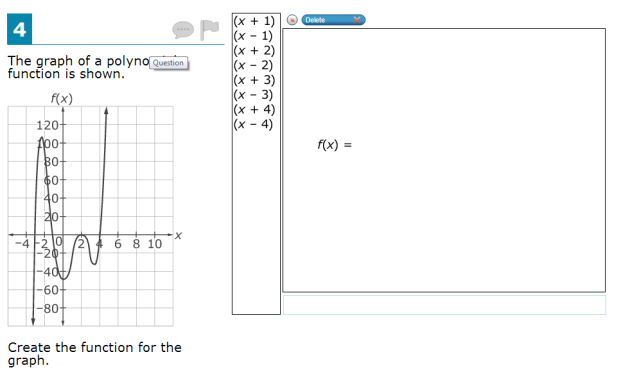
There are several issues with this item. By far the greatest issue is that it doesn’t assess a Common Core standard. The closest standard is HSA-APR.B.3, and read it carefully:

• HSA-APR.B.3: Identify zeros of polynomials when suitable factorizations are available, and use the zeros to construct a rough graph of the function defined by the polynomial.

This problem doesn’t ask students to do that. It asks students to use a rough sketch of a graph to build a factorization, identifying the linear factors of the underlying polynomial.

Besides this, there are some serious mathematical issues with this item as presented. The correct answer to this type of problem should start out in one’s mind as a multiple of 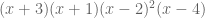, applying the Remainder Theorem (HSA-APR.B.2). Then, you check a sixth point to find the multiple, making sure the polynomial agrees with the nonzero points on the graph (a polynomial function of degree n is determined by n+1 function values, not just its n roots). But no coordinates of a sixth point are given. A student could simply not think of this and get the problem right, or estimate the value of the function at 0 and see if the graph is approximately correct (and get it right), or assume that this is a test and read the minds of the test writers (and get it right). It’s a good thing the graph seems to pass through (0, -48), or there would be no way to give a correct answer!

Even if you could get the exact coordinates of f(0), there are other polynomials functions whose graphs contain these same points and that have an extra x-intercept off the picture. The phrase “the function for the graph” is not accurate: there is more than one. Better wording: “Find a polynomial function that could have this graph.” The phrase “Create the function” should also be avoided, since it’s not clear what it means; Common Core has students “define” a function or “build” a function for modeling or transformation.

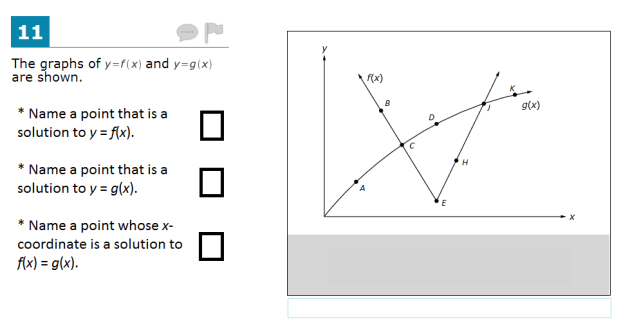
Still, the core issue is that this problem does not directly address a standard. The problem would be much better if it assessed HSA-APR.B.3 directly: Give a function defined by a polynomial that has been partially factored, revealing some zeros, allowing for complete factorization. For example:

Students who can sketch the graph of g (or answer questions about the graph) have met several HSA-APR standards.

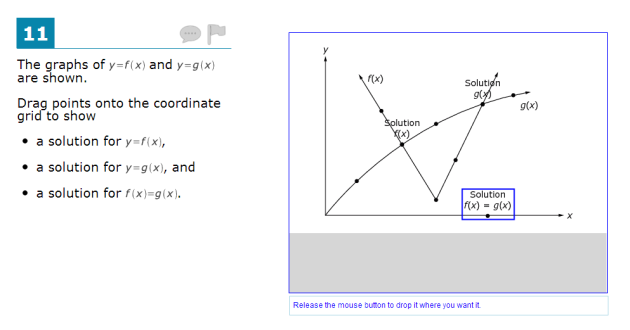
Separate from the mathematics, there are a few major interface issues with this problem. Students are only allowed to drag linear factors to the right, so it is not possible for a student to enter . They must instead enter the clumsy . Some students will wonder why they have to do it this way, others will think the interface is broken. It’s an unnecessary hurdle that will prevent some students from answering correctly even though they are capable of completing the task on paper.

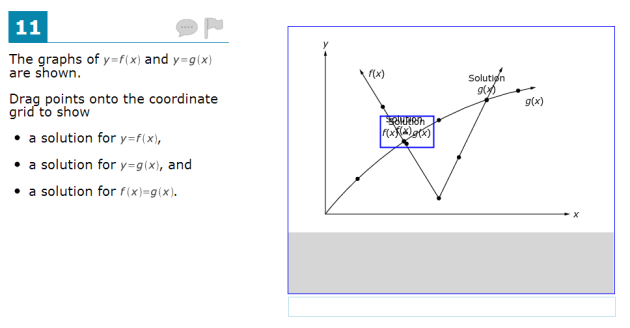
Like #11, the interface does a poor job of overwriting when new objects are placed. Dragged objects “snap” into one of five positions, and if an object is already there, conflict:

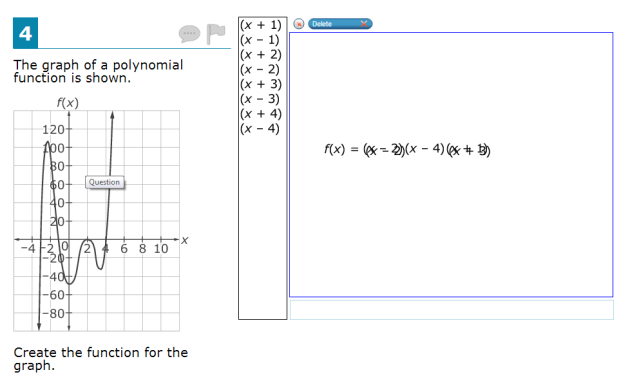
We can picture a student trying to do this on purpose, attempting to get the 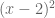term. It easily happens by accident and the interface for “deleting” objects is not obvious. Would the answer above be marked correct or incorrect? It’s not clear, and that is a big problem.

The SBAC Practice Tests are available for public viewing, and we are grateful to have these problems available for public comment.

[Testing Testing] SBAC Grade 11 Practice Test #11

Each “Testing Testing” post will analyze a released test item, focusing on both the mathematics and interface involved in the new breed of SBAC and PARCC exams. Interfaces can have huge effects on how problems are posed, read, answered, and scored. Posts will also provide suggestions on how to improve these exams, in terms of the mathematics presented, and also in terms of the interface students will use when taking exams.

Here’s Problem 11 from the SBAC Grade 11 Math Practice Test.  (A colleague suggests I have chosen Problems 7 and 11 as the first examples primarily because I love Slurpees.)

This problem targets HSA-REI-D.10 and HSA-REI.D.11, knowing that the points on a graph are the solutions to the corresponding equation, and that the x-coordinates of the points where the graphs of y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x).

There is one mathematical error in the problem. When asking for “a solution for f(x) = g(x)”, the answer is an x-coordinate, not a point — something HSA-REI.D.11 states explicitly. This placement of points should be correct:

The problem interface will not allow the third point to be placed here. A placed point “snaps” to the nearest marked point on the grid. These interface behaviors need to be described in the problem, or the results can be surprising or frustrating. For example, a student might want to place their solution to y = g(x) at (0,0). The problem doesn’t exclude them from doing this, but the interface does.

The interface also causes trouble when points are placed atop one another. It looks like this:

Note that the newly placed point is not in the same position as the original. I can’t tell whether or not this solution would be accepted on the exam, and fixing the problem requires moving away the new point, then the old point, then replacing the new point. It’s a mess. If the exam requires all three points to be different from one another, this needs to be part of the problem statement, and the interface should “push” old points back to the gray area at the bottom if a new point is placed in the same location.

These interface issues can be fixed. Eliminate the dragging, label each target point in the grid, and ask the questions about the specific points. This also allows more explicit asking about HSA-REI.D.11 rather than the previous “solution for f(x) = g(x)”.

This new version keeps alive what makes the original question better than multiple-choice: there are several correct answers to each part. One might consider changing this version (or the original) to require the student to provide points that are on the graph of one function and not the other: “Name a point that is a solution to y = f(x) but not y = g(x)”.  Otherwise, a student can answer all three questions correctly with “C” without assurance that they have mastered the standard.

The SBAC Practice Tests are available for public viewing, and we are grateful to have these problems available for public comment.