April 25, 2011
by Bowen Kerins
Regardless of the course, non-monic factoring was always a thorny issue in my teaching. My students never seemed to get “good” at it, even though they seemed alright at monic factoring (“monic” just means the first coefficient is 1, like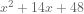 
). This topic made me really question why I was teaching it, for several reasons:
- The very next thing was the quadratic formula, and for most of the things non-monic factoring could be useful for, I felt the quadratic formula would be just as good.
- I couldn’t find many places later in my curriculum where non-monic factoring was being used, so it seemed like a topic taught for a single purpose.
- The methods I saw for factoring non-monic quadratics had little or nothing to do with the methods for factoring monic quadratics.
- The method I learned and first taught amounted to trial-and-error.
And maybe you know this method too: to factor 
, you write down all the factors of 6, separately write down all the factors of 35, and start making pairs. Eventually you either find the pair that works, or you run out of pairs:
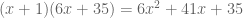, nope
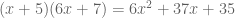, nope
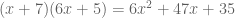, nope, keep trying…
And I was polite in picking 6 and 35 here, two numbers with only two prime factors each! I feel this method is a mathematical nightmare. Keep testing, keep checking. And don’t give the ones that aren’t factorable, since the only way to know it’s unfactorable is to test all the possibilities, and that’s just mean.
A year or two later, I learned and taught the “key number method”: multiply the coefficients of “a” and “c” (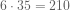
). Then you break up the middle term (
) into two pieces whose coefficients multiply to 210:
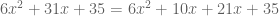
Then “group” in pairs and a miracle occurs:
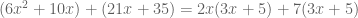
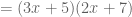
This worked a lot better for my students, by which I mean they got correct answers faster and with greater accuracy. But the core of this method is the “miracle” that splitting the in this exact, specific way will do great things. It works because it works. (There are better explanations, but my students just memorized what to do.)
One advantage of the key number method is it can be applied to monics, too, visualizing the “sum and product” concept:
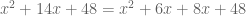
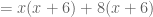
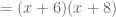
But this generally comes after the fact: I didn’t teach students to factor monics in this way.
While working on CME Project, I learned (through Al Cuoco and Jeremy Kahan, a field test teacher) about a “scaling” method that uses monic factoring as the core of non-monic factoring. It feels a lot more natural, cements monic factoring, and fits tightly with Mathematical Practice #7, “Look for and make use of structure.” It starts with specific non-monics like this one:
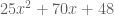
Try factoring that for a second using either of the methods presented above. It’s messy! But, would you believe this is actually a monic quadratic? It’s just got a different variable: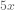 
.
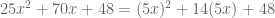
Now cover your finger over each 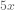: it reads 
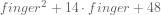. Doesn’t matter what’s under the finger: it factors!
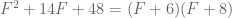
And you’re done when you lift your finger, remembering that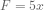 
. In teaching, I used capital letters for these substitutions, to remind students that there was more work to be done later.
How fast was that? And understandable, too! The core concept of a replacement of variable (the book calls this “chunking”) plays forward deeply into later topics and courses: when I say I used capital letters for substitutions, I generally was doing that with Precalculus or Calculus students, but the concept can be seen much, much earlier. By using it frequently, it becomes a tool students actively look to use when they see something complicated.
But I fudged the example: it’s got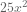 
. How about that original one, ? It doesn’t have a perfect square term, but … wishful thinking … we can make one by multiplying through by 6, then paying it back later.
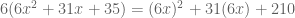
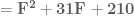
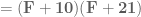
Note that this method includes the step that was part of the “key number method”: the 210 is produced by multiplying the coefficients of “a” and “c”, but this time there is a more mathematical reason for doing so. And the payoff is the same, since we then need two numbers that add to 31 and multiply to 210 — but we use the monic factoring method to perform that step. This cements monic factoring skills, as it becomes part of the process in the later topic. And now the miracle, as we have common factors in the two right-side terms:
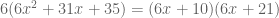
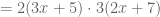
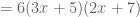
And now you zap the 6 from each side and you’re done:
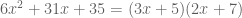
It was shocking to me that this method works at all, and especially shocking that it always works: any factorable non-monic quadratic can be dealt with using this method. And variable substitution is a natural method used in other places: completing the square is a variable replacement using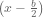 
as the variable … 
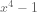is a difference of squares … circles and ellipses all relate to the unit circle 
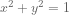… trigonometric equations are just regular equations when you cover your hand over the “
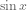” part … a z-score is a linear substitution … and others.
The biggest benefit of presenting substitution methods as early as possible is that students learn a general-purpose tool they can apply repeatedly across grades and topics. I also think it makes quadratic factoring easier and faster to teach. What do you think?
Next: how this method can be used to develop the quadratic formula…
(If you know how to better display equations easily in places like this, let me know. The LaTeX equations look pretty bad in the vertical alignment category, and I had to force a white background on each equation. As long as it’s readable, I guess, but somehow I think it could be better. Thanks to Mark Betnel for the pointer to the LaTeX commands available.)
Patterns in Practice 